This combines a couple of old posts that I recently revisited – because the challenges remain! Working with teachers from primary to FE, I’ve found it fascinating to consider the areas of maths that students find difficult and the processes we need to consider when teaching them to overcome these difficulties. It seems to me that, when students struggle, the key challenge is to get the balance and sequencing right between time spent building more secure routines and time spent developing more secure, fundamental mental models. Sometimes, the fundamentals emerge after lots of practice; sometimes the models need to come first for the routines to make any sense. The really tricky bit is that this varies for different concepts and different learners.
I don’t have a neat set of proven strategies here; I’m just going to share some of the things I’ve discussed with maths colleagues as a non-specialist over the years. It’s more a list of questions and observations than solutions. If you teach maths you may find all of this blindingly obvious but, here, I’m an outsider looking into your world.
Times Tables and Division
At a primary-secondary Transition Forum, this was a key topic. We discussed the reasons behind children arriving to Year 7 without secure knowledge of their tables. From the primary perspective, this isn’t for want of trying. Routine recall tests are ubiquitous; they practise them all the time. Secondary teachers often use times tables tests as lesson starters (one example being the excellent Times Tables Rock Stars developed by Bruno Reddy https://ttrockstars.com/ @MrReddyMaths) ; but even at KS4, not every student is secure. Crucially, the insecurity is strongest in division mode (eg 56÷8=7). There seems to be a need for a stronger emphasis on the mechanics of multiplication (eg array of 56 made from 8 rows of 7) as well as locking-in rote recall.
When students in Y8 are struggling with short division, they’re often confused by the language; they use 56 divided 8 and 8 divided by 56 interchangeably; the idea that finding ‘ how many 8s go into 56’ is the same as ‘divided by’ isn’t obvious to everyone. It’s more tricky when they are faced with remainders: eg how many 8s go into 54 – being able to see quickly that it is 6 with a remainder. Weaker students still count up..8,16,24,32,40,48…56 is too far – which slows them down enormously, as opposed to homing in on 48 as a known multiple and then finding the remainder.
A suggestion from one primary teachers was that tables should be learned four ways all of the time, all mixed in. 8×7, 7×8, 56÷8, 56÷7. We don’t do enough division early on so some children might see the operations as separate. Rote chanting and all the wall charts that count up in 5s, 6s and so on, don’t emphasise the reciprocal patterns or the divisions enough.
Dividing by 10. Place value and knocking noughts off.
In one lower sets, I am often fascinated with the struggles over this. 70÷10=7; 40÷10=4 no problem. But 10÷10? Baffling. How could it be 1? The idea of a number being divided by itself seemed to throw them. How many 5s in 5? It just seemed weird to them.. they wanted so say 5? There’s just five. Not 1. One 5 in 5; one 10 in 10 – this isn’t obvious to everyone! In terms of the method, we’ve talked about the understanding of dividing by 10 in terms of shifting the decimal point, moving down in powers-of-10 base units and the practice of knocking noughts off. There’s the awkwardness that a deeper method based on place value leads to students writing 70÷10= 7.0 which isn’t appropriate for integers – but the ‘knock a nought off’ short cut works, even though it is less rigorous as a general rule. Adding units and currency adds another dimension. £8 divided by 10 yield incorrect answers of £0.8 and ‘8p’ instead of £0.80 and 80p. Meanwhile 8kg ÷10 is 0.8kg. The need for the extra zero for currency but not for other units is a source of confusion.
10% of 10 is 1: What’s 20% of 20?
The problem with 10% is that it is a special case where dividing by 10 is the same as multiplying by 10/100. If students repeat the wrong pattern, they get confused. I’ve seen 20% of 20 as 1 (20/20) and 2 (just multiplying up by 2). The link from percentages to fractions is important here: 100= 5×20; 20% is equivalent to 1/5; 25% to 1/4 and so on. Repeated mechanical operations with 10% can undermine rather than reinforce the general concept.
Reverse Percentages
This is tougher than it looks. If Something bought with 30% off costs £84, how much was it originally? Recognition that the £84 is 70/100 or 0.7 of the original is needed. The intuition that the answer is £84÷0.7 isn’t that straightforward. Conceptually it is easier to go through £84 = 70%, so 1% is £84/70; then 100% is then 100 x the answer. However, with increases (eg the wages went up by 12% to £280, what were they before) some students seem to struggle with the ‘find 1%’ model; it’s easier for them to see 1.12 as a scale factor to divide by. There’s something about dividing by numbers smaller than 1 that makes students doubt themselves whereas dividing by a number bigger than 1 seems logical.
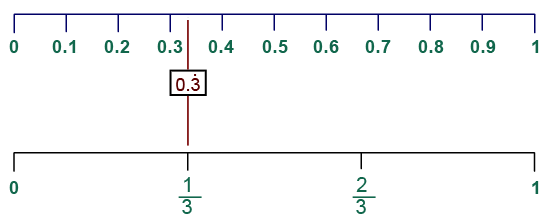
Fractions and Decimals on the Number line
How intuitive is it that 2/7, 3/10, 4/10 and 3/7 are in ascending order? It is if you convert to a common denominator ( 20,21, 28 and 30 70ths respectively) or decimals – 0.29, 0.3, 0.4, 0.43. The jump from slices of pie and shaded squares in a grid up to the number line is really important and sometimes difficult to make. I find that some students have a weak mental model of fractions as decimals; that ability to estimate relative value. For some it’s as though 5/8 has no actual size – it is just a sum to perform. I’ve said in another blog post that the number line is probably the most important diagram of all time; a trick seems to be to make students as happy with the 0.00 to 1.00 scale as they are with the 0 to 100 scale. It’s more of a leap than it should be at first glance.
Rules and Short-Cuts.
My son asked me recently what -1÷ -1 was. He said ‘do you just cancel the minuses or is it true because any number divided by itself is 1?). We talked about multiplying both top and bottom by -1 (ie by the same thing) so that you get 1 ÷1. Then he could see how it all linked. He was losing the logical link with other operations after repeated application of the ‘minuses cancel’ short-hand.
This happens with simple rearrangement of equations. x + 2 = 10 leads to x = 10 -2. Often students and some teachers talk about ‘taking the 2 over to the other side’ instead of the more fundamental idea of ‘subtracting 2 from both sides’. Similarly with something like x = 60/ y; This means that xy = 60. We have not just ‘taken the y over to the other side and put it on top’; we’ve multiplied both sides by y. I think we need to careful not to lose the fundamentals in the short-cuts because students come unstuck later on.
Another one of these is with common denominators and cross-multiplying when adding and subtracting fractions. With students who are struggling with adding fractions (even in Y11) it’s fair enough to focus on the drill: cross-multiply because it works every time.
3/4 + 5/11 will be found by writing (3×11 + 5 x4)/44. It works. However, the fundamentals of finding a common denominator by appropriate selection of a multipliers for both numerator and denominator – can be lost. That understanding is necessary for some algebraic fractions and higher order questions where cross multiplying makes things more complex instead of factorising the denominators and simplifying.
A final area under this category is in column subtraction versus chunking. If you’re asked to find 328 – 189, it’s easy to break it up: 11 up to 200, + 100 and a further 28 makes 139. Done. However, this isn’t always sensible or easy so the column version with borrowing and carrying of 100s, 10 and units is important too. How much time to give to each method? That’s a tough one with lots of variables but it must be both in combination.
Equations. Putting the numbers in; the concept of variables.
As a physics teacher I know full well that some students benefit hugely from repeated use of triangles like S=D/T and V = IR. They can use them in different arrangements to bang the numbers in long before they really understand the physics. Voltage and Current are basically ‘electricity’ to lots of people who can still use V=IR. Similarly, in maths, in our discussions we’ve considered whether the concept of forming equations for a new scenario needs to be modelled lots of times before it makes sense in terms of the general concept of ‘variables’ and algebraic substitution.
Find the Salary for d days paid at £12 per day. S = 12d; Find the taxi fare F if it’s £10 per journey plus £3 per mile m; F = 10 + 3m. And so on. Once you see lots of these in action, the concept seems clear. But if you start with the concept, it can seem a bit abstract.
Proof and ‘Show that’
The concept of proof is fascinating. It was great to see the parallel lines proof in a lesson last week. I don’t know if the exterior angles proof is any more fundamental than the alternate angles proof – and they both require some ground work to show that some basic concepts are defined and don’t require proof. In the appropriate context, they’re both worth doing as is the simple but wonderful act of ripping all the corners off ANY triangle so show they form a straight line. But before you explore any specific proof, it seems that you need to explain why things needs to be proven at all. The angles in a triangle add up to 180 because they just do; it’s a fact we’re told. That’s where kids often start from.
It was interesting to see students struggle with text-book questions linked to formulae that were posed as “Show that” S is £36 if the man works for 3 days. They wanted to use the number 36 in the calculation rather than see this as the answer to be found. ‘Show that’ isn’t intuitive it appears.
Powers of 10...scaling number bonds up and down.
I’m interested in the extent to which students find it hard to move beyond certain limits of numbers even though all the basic patterns are replicated at higher or lower orders. 33 and 67 are bonded to 100 (if that’s the phrase); 325 and 675 are bonded to 1000. So far so good. 303 and 697 – got it. But 3034 and 6966 as bonded to 10000 or a similar delve into decimals can seem confusing – especially with stray zeros. My feeling is that children spend too long in the comfort of the 0-100 range at an early stage; that is probably because it feels necessary to secure understanding there as a platform. However, I’d suggest we need to be bolder and Go Big and Small earlier.
In a Y8 science lesson last term I was asking students to imagine how many atoms were in small droplet. They went from a million to a billion to 10 billion… but then they could only imagine multiples: 20 billion, 30 billion… no longer going up in powers of 10. It was as if they’d reached a conceptual ceiling with how big numbers can get. That was fascinating. Beyond about 50 billion it was just “really really big; bigger than I can imagine”. And the same goes the other way.
Algebra:
As a teacher I was once dismayed to discover how many of my students got the answer wrong to:
Simplify t2 + t2.
Most of them had written t2 + t2 = t4 instead of t2 + t2 = 2t2
This was in a synoptic test, a few weeks after we had covered this topic in class. At the time, in the lessons, they were whizzing through this stuff. I had built it up slowly. pen + pen = two pens; 4 + 4 = 2×4; p + p = 2p and so, obviously, t2 + t2 = 2t2.
At the time, they were all seemed secure with this. Any term + the same term = two x that term, including more complicated terms:
pt2s3 + pt2s3 = 2pt2s3
If’ we had stopped there, they would probably have been ok. But we had also gone further, exploring indices and patterns such as this:
t x t = t2
t x t x t = t3
t x t x t x t = t4
(t x t) x (t x t) = t4
t2 x t2 = t4
Even though, at the time, we had practised various variations of this and students were getting questions right, evidently this was not making a shift in their mental models. That final line introduces the link between t2 x t2 and t4 . In their world, largely governed by surface learning, that connection is strong enough to override their thinking around the operations + or x. It is common for them to want to remember answers rather than methods so t2 + t2 = t4 beat t2 + t2 = 2t2.
Perhaps it was because it was the most recent thing we’d done in algebra; perhaps it was because it feels more sophisticated to write t4 , but, regardless of the reason, I learned that their mental model for the whole business was weaker than I realised. When faced with a question, garbled surface recall dominated over deeper conceptual understanding. Once you put numbers in it always more obvious; they get that 9 +9 is not the same as 9 x9. But, in algebraic form, the abstraction overrides their number models.
One girl even stubbornly challenged me. No! That’s wrong sir. t2 + t2 IS t4 . The way she had remembered it instead of understanding it was so strong, she didn’t believe me. We had to go over it all again, step by step. I had to pull down her badly remembered model, fixed firmly in her head to replace it with mine. This told me that I hadn’t done enough of that. We need to mix up the questions, use more wrong answer/spot the mistake questions in future and, generally reinforce the meaning of the algebra over and over again.
Another example came from a simple introductory exercise around making formulae to solve problems. For example, writing a formula for the perimeter of a shape. The diagram given was this. Write a formula for the perimeter in terms of s.
One of my students had written P = 4 + S. This took be aback. Her explanation: there are four sides, so you add four to S to get the perimeter. She hadn’t simply replaced a times with a plus. We talked about how S was a length… 4 is a number of sides; they are numbers on different scales, doing different jobs. This seemed beyond her. It made more sense when we labelled the diagram fully: 
Now she could see it was S +S + S+ S = 4 lots of S, hence 4S. So, the problem came from being able to see how the number 4 and the variable S combined. It wasn’t immediately obvious to her that multiplication was the appropriate operation. This is worrying. She’s in Year 10 – but we have to work with the students we have, helping them to develop a stronger sense of the meaning of numbers and mental models for the various operations. The difficulty is that, at this age, they often just want short-cut, surface memory techniques to get through it all and that just isn’t enough.
I could go further: vector addition and first order differentiation were two of the other topics I have observed being taught where the same general pattern of thought applies. What are the fundamentals? What are the short-hand drills? Where do we begin… letting the deeper understanding emerge from the routine practice or to go deep from the start? I think that what matters is that, whichever route is chosen, it is done deliberately. Similarly with all the other conceptual challenges above; if we know where they might be, we might be better prepared to help students overcome them.
Links to previous posts about maths:
1. Level 6 Maths at KS2 – what’s the problem?
2. Owning the problem is part of the solution.
3. https://teacherhead.com/2015/09/26/maths-mindsets-my-y10s/
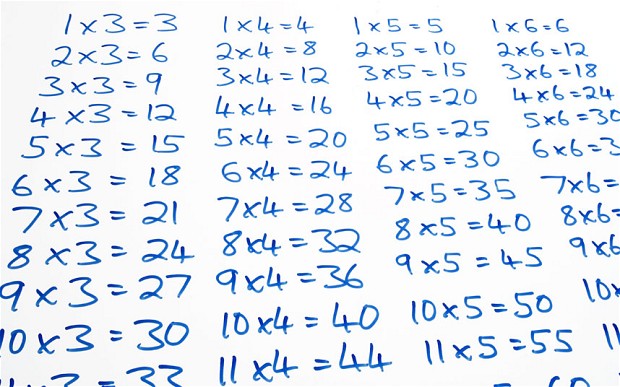


Yes, you explained in the right way that how some students feel some trouble in solving problems of maths and as well your blog explains it very well that how to solve the problems
LikeLike
I teach Algebra 1 and have so many students struggle with combining exponents when adding like terms. I like how you started with objects and related them to mathematical terms. Thanks for the article!
LikeLiked by 1 person